|
|
42.
|
|
|
A small test for the condestsp function: condestsp gives an estimate of 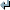
the condition number K1 in 1-norm of a real sparse matrix A: |
|
|
 represents a line break.
Start a new line in the equivalent position in the translation.
represents a line break.
Start a new line in the equivalent position in the translation.
|
|
|
 represents a space character.
Enter a space in the equivalent position in the translation.
represents a space character.
Enter a space in the equivalent position in the translation.
|
|
|
|
|
(no translation yet)
|
|
|
|
|
43.
|
|
|
without explicitly computing the inverse of A. condestsp uses a factorization given by 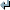
umf_lufact but if you have already computed this one it is recommended to give the pointer to the factorization.
|
|
|
 represents a line break.
Start a new line in the equivalent position in the translation.
represents a line break.
Start a new line in the equivalent position in the translation.
|
|
|
 represents a space character.
Enter a space in the equivalent position in the translation.
represents a space character.
Enter a space in the equivalent position in the translation.
|
|
|
|
|
(no translation yet)
|
|
|
|
|
44.
|
|
|
The test consists in forming small sparse matrices (so as to compute K1 exactly with 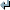
norm(inv(full(A)),1)) whose values are chosen from the normal distribution. |
|
|
 represents a line break.
Start a new line in the equivalent position in the translation.
represents a line break.
Start a new line in the equivalent position in the translation.
|
|
|
|
|
(no translation yet)
|
|
|
|
|
45.
|
|
|
Press Return to continue... 
|
|
|
 represents a line break.
Start a new line in the equivalent position in the translation.
represents a line break.
Start a new line in the equivalent position in the translation.
|
|
|
|
|
(no translation yet)
|
|
|
|
|
46.
|
|
|
This test compares umfpack v3 and sparse v1.3 via their Scilab interface.
|
|
|
|
|
(no translation yet)
|
|
|
|
|
47.
|
|
|
The test consists in loading Harwell-Boeing sparse matrices and solve linear system with a random rhs.
|
|
|
|
|
(no translation yet)
|
|
|
|
|
48.
|
|
|
The matrices presented here come from the NIST server Matrix server:
|
|
|
|
|
(no translation yet)
|
|
|
|
|
49.
|
|
|
Warning: tests 2 and 3 take much more time than the others.
|
|
|
|
|
(no translation yet)
|
|
|
|
|
50.
|
|
|
Test 1: Jacobian of a nonlinear system of ordinary differential equations (ODEs) modeling a laser
|
|
|
|
|
(no translation yet)
|
|
|
|
|
51.
|
|
|
Mean time and accuracy for umfpack (t1 and ||A*x-b||):
|
|
|
 represents a space character.
Enter a space in the equivalent position in the translation.
represents a space character.
Enter a space in the equivalent position in the translation.
|
|
|
|
|
(no translation yet)
|
|
|
